Diminishing returns for more effort
You will be very familiar with the law of diminishing returns, where you get a lot of payback for your initial efforts (sometimes called ‘low hanging fruit’), then you have to work harder for smaller rewards. An example for IT professionals might be a server or application consolidation project. Hacking and Stacking produces good early $ savings, but as you go through the project, you need to work hard to get less reward.- then the ’80/20′ rule comes in to play. This will reveal a simple formula you can use at the early stages of forecasting results in such a project.
Expressing as a formula
In this kind of scenario its hard to come up with a ‘finger in the air’ estimate of what the savings could be when embarking on such a project, since the savings are not going to be linear. I was looking for a simple formula that could be generally applied to such projects and came up with this. (a1 is the value to be diminished, and E1 is the ‘aggressivity’ to apply.
=( SIGN(A2) * $E$1 * (SQRT(2 * (SIGN(A2) * A2 / $E$1) + 1) - 1) )
Function diminishingReturn(val As Double, Optional s As Double = 10) As Double
diminishingReturn = Sgn(val) * s * (Sqr(2 * (Sgn(val) * val / s) + 1) - 1)
End Function
Result
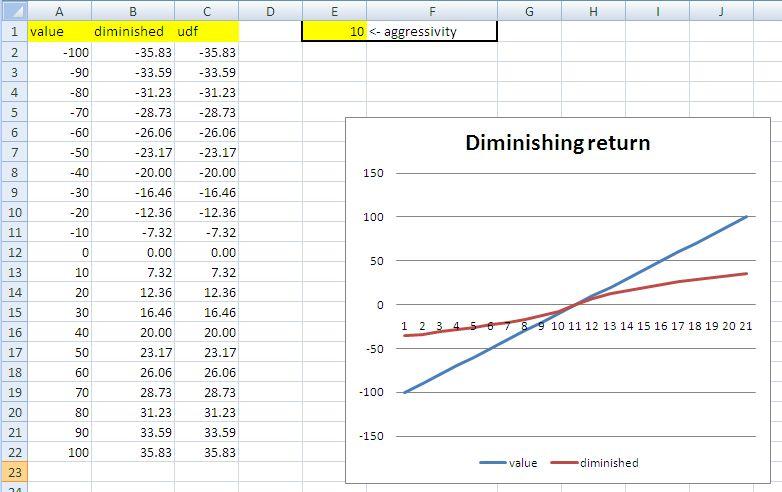
Here is some test data, and you can see the return on investment shown by the red line tails off the higher the investment. You can tune the aggressivity with about 100 starting coming close to a straight line. The only difference between the ‘diminished’ column and the ‘udf’ column is that one uses the formula, the other the UDF version of the formula (the results .. I hope.. are identical)
Downloadable workbook with this example can be found here