This problem is often used to show that statistics are sometimes counter intuitive. If you try to imagine how many people you would need to have a 50% chance of two people sharing the same birthday, you’d probably be surprised to learn that the number is around 23. The formula for calculating that is given in this wiki page, but when you implement this in Excel using factorials, you very soon get a number overflow, so we need another approach. To do that we are going to use the product() , row() and indirect () functions, entered as an array (CSE) formula. This will also start to overflow at about 120 , but we have already converged on a probability of close to 1 by the time we get to 100 people anyway.
Lets say our number of people in the group is in A1, then the (Array) formula is this (it will give the wrong answer if not entered as CSE)
=1-PRODUCT(ROW(INDIRECT(“365:”&366-A1)))/POWER(365,A1)
This gives the probability of .507 of at least 2 people out of 23 sharing a birthday.
Update
I posted this as a challenge on the Excel Hero Linked In forum, and got back a nice solution from Kevin Wright, which of course doesn’t need to be entered as an array formula.
=1-PERMUT(365,A1)/365^A1
So although the array formula shows how the probability is calculated, it does show how reaching for an array solution too quickly makes us forget about some of the powerful built in Excel capabilities.
Extending the problem
In trying to generalize the problem – say 3 or 4 or … k people with shared birthdays in a group of n, I came up with a partial solution
=1-PERMUT(365,A1)/365^A1-COMBIN(A1,B1-1)*PERMUT(365,A1-1)/365^A1
My theory was that in eliminating the pairs and no sharing, we would be left with 3 sharing. However – as per this analysis, this is woefully inadequate and plain wrong. Here’s a plot of probabilities using the methodology described there.
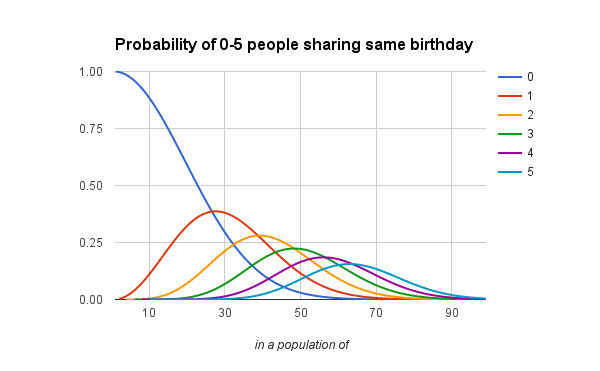
Going back to the drawing board, and using the explanation here, it is of course straightforward to recreate the table referred to in the article
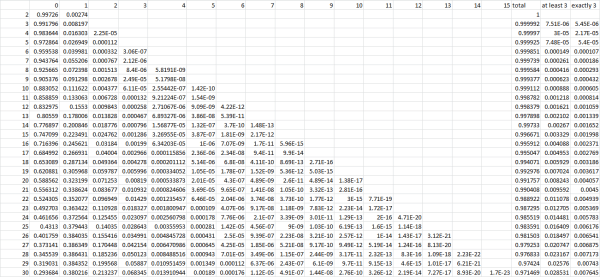
A sample cell contains this formula
=IFERROR(COMBIN(365,G$1)*PERMUT($A23,2*G$1)*PERMUT(365-G$1,$A23-G$1*2)/(2^G$1*365^$A23),””)
The probability of at least three is then just the sum of the row for a given N. However – it is still not generalized for anything other than 3.
Estimation
There are various estimation methods for recursive calculations such as these. I’ll look into these for a future post.
Challenge
Hans Knudsen translated this into an array formula, doing away with the need for a table, as below (group size is in a8)
=1-SUM(COMBIN(365, (ROW(INDIRECT(“1:”&TRUNC(A8/2)))-1))*PERMUT(A8,2* (ROW(INDIRECT(“1:”&TRUNC(A8/2)))-1))*PERMUT(365- (ROW(INDIRECT(“1:”&TRUNC(A8/2)))-1),A8-2* (ROW(INDIRECT(“1:”&TRUNC(A8/2)))-1))/((2^ (ROW(INDIRECT(“1:”&TRUNC(A8/2)))-1)*365^A8)))
This gives the probability of .511 of at least 3 people out of 88 sharing a birthday.This mostly matches the accepted results for this problem of 3 or more sharing, except that the calculation overflows past a group of 113, and it doesn’t work for groups 1,2 or 3 – the answers to which should be 0,0, and some very small number. So the challenge of generalizing this beyond two and three shared birthdays and coming up with a calculation that works for all group sizes still stands. Contact me on our forum if you have some suggestions. For more tips like this see Get Started Snippets.
In the meantime why not join our forum, follow the blog or follow me on Twitter to ensure you get updates when they are available.
