What is this
These few pages are about how to create a Sudoku Solver and Generator using Excel/VBA. If you just want one, then go ahead and download it. If you are interested in how to write a solver and generator, then read on.
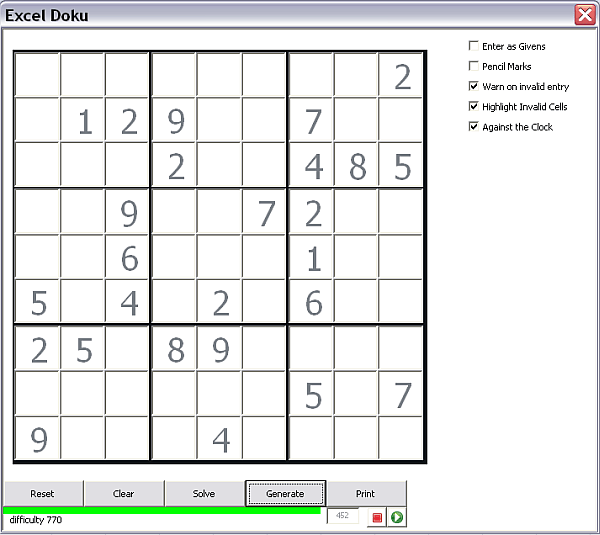
Here is the finished Sudoku Generator and solver.
Design considerations
You will all be be familiar with Sudoku, and no doubt have seen the thousands of solvers, and rather less generators around. I’ve seen a few in Excel also, but not that many. What we are going to do is write one from scratch, and make heavy use of both Classes and Recursion. The files available from the downlable section will reflect progress made so far, and hopefully, eventually a fully functioning solver and generator. I’m calling it ExcelDoku as a working name- any suggestions are welcome. As usual the complete project is downloadable from the downloads page.
This is going to be a fairly complex problems because we are going to do the following
- Deal with sudokus of any shape up to 4 x 4. r x c refers to the number of rows and columns in a Box. The usual Sudoku is 3 x 3 and consists of of 81 cells. We will allow odd shapes like 2 x 5 and so on, since it is easier to generalize that from the start than to try to retrofit.
- Generate genuine puzzles, on the fly, which can be solved by human sudoku strategies – ie. not by ‘brute force trial and error
- Allow generation to a target level of difficulty – easy, medium, hard, diabolical – where the difficulty is based on the complication of the strategies required to solve, rather than just the number of starting cells.
Implementation considerations
The capabilities a solver and generator like this needs are as follows
- Solve puzzles using human Sudoku Strategies
- Solve puzzles using ‘brute force’ in order to be able to generate skeleton puzzles – this is essentially solving a ‘blank puzzle’
- User interface to show solved puzzles, allow interactive solving, show pencil marks, select options, enter custom puzzles, and show generated puzzles
In terms of priority, our first priority is to create a basic solver – since this is needed to help generate and to validate generated puzzles. The user interface will be kept skeletal until we have a solid solver and generator, especially since our objective is to demonstrate recursion in the first instance.
Some comments on recursion
If you have followed the roadmapper project you will have seen examples of recursion with emphasis on dealing with variable depths of parent/child relationships. We are going to look at backtracking here. You will find that backtracking is used in routing in games, or in navigation systems. Backtracking is required when, as a result of some change you make to an item you are processing, the assumptions you had originally made about that item are no longer valid – so you need to go back and try something else – an alternate path. Recursion is a great fit for dealing with that.
In our Sudoku solver, recursion is going to be most useful for
- Backtracking during a ‘brute force’ solution. This would happen when we run out of options for trying out a value in a box, so need to go backwards until we find an alternative arrangement of numbers that allow us to go right through to a solution
- Backtracking during a ‘strategy solve’. Since we are planning to generate puzzles according to their difficulty, we have to ensure that we exhaust all the easier strategies first. That means that if we resort to a more complex strategy to solve a particular cell, we need to backtrack to apply the result of the newly solved cell to each of the other cells using the easier strategies again.
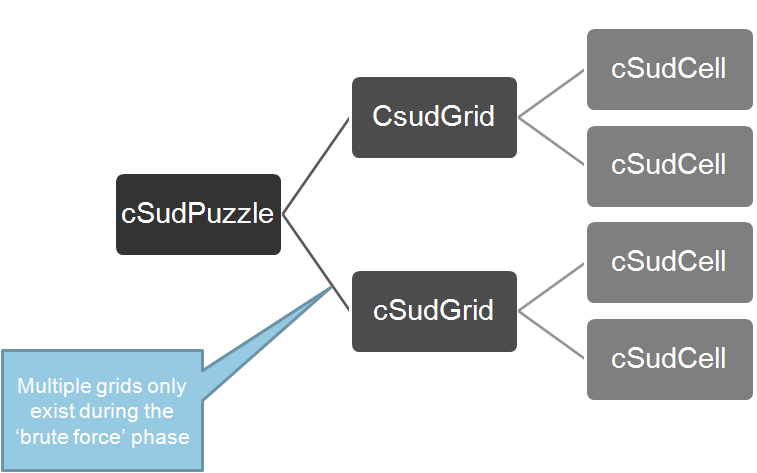
Classes
We will be making extensive use of classes. I cannot emphasize enough the tight relationship between recursion & class encapsulation. Using recursion can get complicated really quickly. Using classes helps to ensure that your procedure is operating on the correct instance of your data. For example in the solver, one of the classes is cSudGrid . This is an object that will represent a complete grid. During ‘brute force solutioning’ (which is the basis of generation), many copies of candidate grid are generated and discarded in a recursive solving procedure. Encapsulating everything in a candidate grid instance simplifies the whole process of creation and discarding. Here is the object model showing the main classes
For help and more information join our community, follow the blog or follow me on Twitter